Spis treści
Pierwiastkowanie to działanie odwrotne do potęgowania. Odpowiada nam na pytanie: Jaką liczbę trzeba podnieść do potęgi b (pomnożyć b razy przez samą siebie), żeby otrzymać liczbę a.
Co to są pierwiastki i co o nich wiedzieć?
Na przykład kwadratowy √4 (pisany z 2 lub bez niej nad znakiem √), czyli jaką liczbę trzeba podnieść do drugiej potęgi, żeby otrzymać 16, odpowiedzią na to pytanie jest 4, bo 4² to 16.
√16 = 4
Z pozoru nie wygląda to na skomplikowane, zwłaszcza jeśli posługujemy się płynnie tabliczką mnożenia. Jednak jak zawsze w matematyce, każde działania możemy skomplikować.
Zanim jednak do tego przejdziemy warto zwrócić uwagę na kilka technicznych aspektów. Po pierwsze, liczba nad pierwiastkiem mówi nam do jakiej potęgi podniesiona została szukana liczba, żeby uzyskać liczbę pod pierwiastkiem. Najbardziej standardowym pierwiastkiem jest pierwiastek kwadratowy, czyli np. wspomniane już √16. Pierwiastki kwadratowe są najczęściej używane, dlatego też możemy pominąć pisanie dwójki nad pierwiastkiem.
Warto o tym pamiętać! Po drugie pierwiastkowanie i działania na pierwiastkach wymaga dobrej znajomości potęgowania i mnożenia, więc upewnij się, że dobrze rozumiesz poprzednie tematy ze szkoły.
Czytaj również: Liczba rzeczywista, wymierna, niewymierna, naturalna i całkowita – definicje, przykłady
Ułamki dziesiętne - jak je zamienić na zwykłe?
Ułamki zwykłe - czym są ułamki właściwe i niewłaściwe i jak dodawać ułamki?
Wzory potrzebne do pierwiastkowania
Działania na pierwiastkach opierają się na kilku bardzo ważnych wzorach, które należy zapamiętać i które postaramy się tu przybliżyć. Pierwszymi podstawowymi wzorami są:
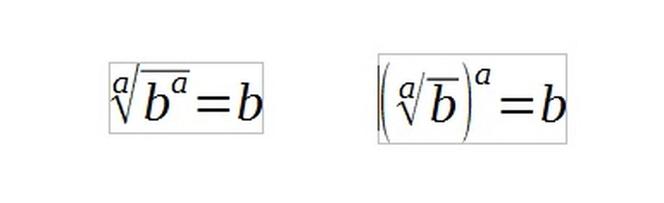
i
A więc, jeśli pod pierwiastkiem znajduje się liczba podniesiona do jakiejś potęgi lub cały pierwiastek jest podniesiony do jakiejś potęgi, a także potęga i stopień pierwiastka są takie same – wtedy pierwiastek równa się liczbie pod pierwiastkiem. Jest to spowodowane tym, że potęgowanie i pierwiastkowanie to działania odwrotne.
Na przykład:
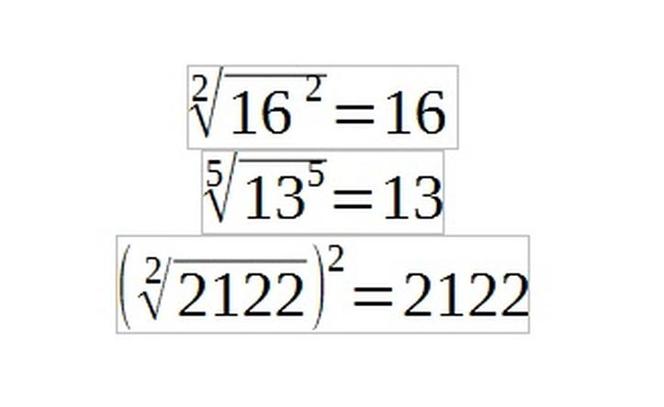
i
Kolejne zasady mówią o tym, że pierwiastek iloczynu, to to samo co iloczyn pierwiastków, a także pierwiastek ilorazu, to to samo co iloraz pierwiastków.
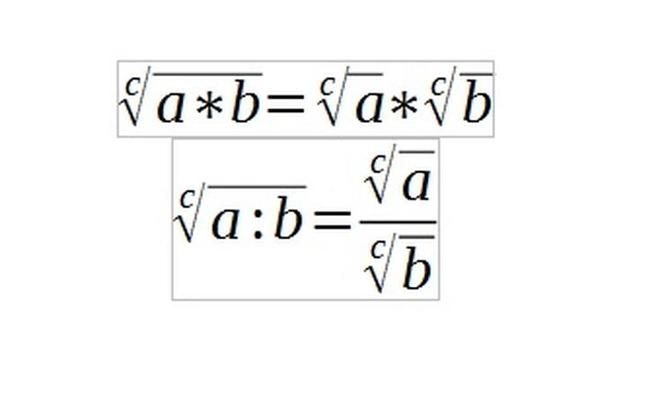
i
W jakich sytuacjach takie wzory są przydatne? Rozważmy taki pierwiastek: ∛27x8
Łatwo moglibyśmy stwierdzić, że jest to to samo co ∛216, jednak to nie pomaga nam za bardzo w rozwiązaniu tego działania. Mając jednak powyższe wzory możemy rozbić jeden duży pierwiastek, na dwa mniejsze, które będziemy w stanie bez problemu rozwiązać. A zatem:
∛27x8=?
∛27x∛8 =?
3x2=6
Możemy też szukać tych wzorów tam, gdzie nie jest to zupełnie oczywiste, np.: √36
36 to inaczej 4x9, czyli √36=√4x9
A to, jak już wiemy, równa się: √4x√9=2x3=6
Przede wszystkim jednak wzory te służą nam do uproszczenia pierwiastków, których nie jesteśmy w stanie w pełni wyciągnąć. Weźmy np. √24.
Żadna z liczb całkowitych podniesiona do kwadratu nie da nam liczby 24. Możemy jednak zauważyć, że √24 to nic innego jak √4x6, a to równa się √4x√6-2x√6.
√6 nie da nam wymiernego wyniku i dlatego 2√6 to liczba, która jest wynikiem, który możemy spokojnie podać jako ostateczny wynik powyższego działania.
