Spis treści
Trapez to czworokąt wypukły, który ma przynajmniej jedną parę boków równoległych. Te boki nazywamy podstawami trapezu. Pozostałe dwa boki nazywane są ramionami trapezu, natomiast odległości między podstawami nazywa się wysokością trapezu. Trapez ma dwa ramiona, dwie podstawy (górną i dolną) i co najmniej jedną parę boków równoległych. Zobacz, jak obliczyć pole trapezu.
Wysokość trapezu
Wysokością trapezu nazywamy odległość między jego postawami, a linia środkowa trapezu to odcinek łączący środki ramion trapezu. Trapezami zatem są: prostokąty, kwadraty, równoległoboki i romby. Odwrotnie niestety nie zawsze jest tak samo.
Przekątne trapezu nie dzielą się na połowy. Wyjątkowym przypadkiem trapezu jest z kolei prostokąt. Ma dwie pary boków równoległych oraz wszystkie kąty wewnętrzne proste. Prostokąt jest zatem trapezem równoramiennym i prostokątnym.
Rodzaje trapezów:
- Trapez dowolny – czyli każdy bok jest innej, różnej, dowolnej, odmiennej długości. Tu przekątne też są różnej długości.
- Trapez prostokątny – czyli przynajmniej jedno ramię jest prostopadłe do podstaw. Prostopadłe ramię jest również wysokością. Posiada kąt wewnętrzny 90º. Prostokąt i kwadrat są trapezami prostokątnymi. Ma dwa kąty proste. Nie ma osi symetrii, lecz ma dwa różne przekątne.
- Trapez równoramienny (ale nie równoległobok). W trapezie tym katy przy podstawie są równe. Przekątne trapezu są równej długości. Ma dwie pary równych katów. Suma kątów ostrego i rozwartego wynosi 180º. Ma jedną oś symetrii. Ma też dwie równe przekątne.
Pole trapezu - jak obliczyć pole trapezu?
A teraz pole trapezu – dokładne objaśnienie tematu:
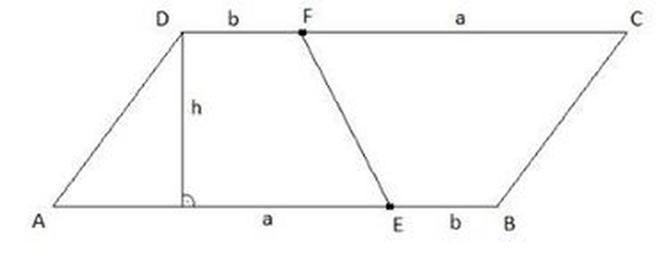
i
a + b = suma długości podstaw trapezu
Jak widać na powyższym rysunku, równoległobok ABCD otrzymaliśmy z dwóch przystających (takich samych) trapezów: trapez AEFD i trapez EBCF.
Pole równoległoboku ABCD jest równe według rysunku:
PRÓWNOLEGŁOBOKU = (a + b) · h
Równoległobok składa się z dwóch jednakowych trapezów, a więc pole trapezu jest równe:
PTRAPEZU = 1/2 · ( a + b ) · h
Pole trapezu jest równe połowie iloczynu sumy długości podstaw i jego wysokości.
Czytaj: Pole trójkąta równobocznego - wzór
Pole trapezu - wzór na pole trapezu
Pole trapezu - zadania
Zad. 1.Dłuższa podstawa trapezu jest równa 4dm, a krótsza stanowi 3/5 długości dłuższej podstawy. Wysokość trapezu jest równa 25cm. Oblicz pole trapezu.
Dane: a = 4dm, b = 3/5 · 4dm = 12/5 dm = 2 · 2/5 dm = 2,4dm, h = 25cm = 2,5dm
Szukane: PTRAPEZU = ?
PTRAPEZU = 1/2 · ( a + b ) · h
PTRAPEZU = 1/2 · ( 4 + 2,4 ) · 2,5 = 1/2 · 6,4 · 2,5 = 3,2 · 2,5 = 8dm2
Odp. Pole tego trapezu wynosi 8dm2.
Zad. 2.Pole trapezu wynosi 54cm2. Podstawy mają długości 8cm i 10cm. Oblicz wysokość tego trapezu.
Dane: PTRAPEZU = 54cm2 , a = 10cm, b = 8cm,
Szukane: h = ?
PTRAPEZU = 1/2 · ( a + b ) · h
54 = 1/2 · ( 10 + 8 ) · h
54 = 1/2 · 18 · h
54 = 9 · h
h = 6cm
Odp. Wysokość tego trapezu wynosi 6cm.
Zad. 3.Pole trapezu jest równe 88cm2. Dłuższa podstawa wynosi 12cm, a wysokość 8cm.Oblicz krótszą podstawę trapezu.
Dane: PTRAPEZU = 88cm2 , a = 12cm, h = 8cm,
Szukane: b = ?
PTRAPEZU = 1/2· ( a + b ) · h
88 = 1/2 · ( 12 + b ) · 8
88 = 4 · ( 12 + b )
88 = 48 + 4b
4b = 88 – 48
4b = 40
b = 10cm
Odp. Krótsza podstawa trapezu wynosi 10cm.
Aby prościej i szybciej zrozumieć temat, zajrzyj do artykułu o polu rombu.



![Dyktando klasa 4. Jakie zasady? Pobierz dyktanda dla klasy 4 do wydruku [PDF]](https://cdn.galleries.smcloud.net/t/galleries/gf-cktd-yP6X-DcZN_chlopiec-pisze-przy-biurku-994x828.jpg)
![Dyktando klasa 2. Jakie zasady? Pobierz dyktanda dla klasy 2 do wydruku [PDF]](https://cdn.galleries.smcloud.net/t/galleries/gf-rLv5-E6e3-QzpE_chlopiec-przy-biurku-300x250.jpg)


