Ułamki zwykłe to obowiązkowy dział matematyki w szkole podstawowej. Warto żebyś zrozumiał ten temat, bo ułamki czy to zwykłe, czy ułamki dziesiętne, nie są tylko tematem kolejnej zdalnej lekcji. Będą ci towarzyszyć przez resztę twojego życia w każdej jego dziedzinie. Nie wierzysz? Zaraz ci to udowodnimy.
Spis treści
- Co to są ułamki zwykłe?
- Ułamki zwykłe - właściwe
- Dodawanie i odejmowanie ułamków zwykłych
- Sprowadzanie ułamków zwykłych do wspólnego mianownika
- Dodawanie ułamków o różnych mianownikach
- Ułamki niewłaściwe i liczby mieszane
Co to są ułamki zwykłe?
Po pierwsze musimy ustalić, czym tak naprawdę są ułamki. Ułamek to inaczej jakaś część całości. Do tej pory w szkole pokazywali ci głównie działania na liczbach całkowitych, czyli na całościach. Liczyliście kilometry, minuty, dekagramy, cukierki albo jabłka.
Czasem jednak mieliście tylko pół jabłka, przeszliście tylko pół kilometra i kupiliście tylko pół kilograma cukierków. W takiej sytuacji liczby całkowite mogą wam nie wystarczyć. Tu właśnie przychodzą z pomocą ułamki. Posłużą nam do przedstawienia połowy jabłka, za pomocą liczb.
Ułamki zwykłe - właściwe
Żeby zrozumieć ułamki zwykłe wyobraź sobie coś, co da się podzielić na równe części. W książkach od matematyki najczęstszym przykładem jest pizza czy ciasto. Da się je podzielić na równe kawałki i wszyscy umieją je sobie wyobrazić, więc trudniej o ewentualne nieporozumienia. My też pójdźmy tym tropem.
Wyobraźmy sobie pizzę podzieloną na osiem równych kawałków. Jeśli zjemy trzy z nich, mówimy, że zjedliśmy 3/8 (czytamy trzy ósme) pizzy – czyli trzy z ośmiu kawałków pizzy.
Cyfra na dole od kreski, którą nazywamy kreską ułamkową, to mianownik. Mianownik mówi nam na ile równych części podzieliliśmy naszą całość (np. na ile kawałków podzieliliśmy pizzę). Licznik (liczba powyżej kreski ułamkowej) mówi, ile kawałków całości nas interesuje.
Kreska ułamkowa jest również tym samym co znak dzielenia. Z lekcji dzielenia wiesz, że 8:8=1. Tak samo 8/8=1, bo osiem kawałków pizzy podzielonej na osiem części, to po prostu jedna pizza. Pamiętaj, nie mówimy to o ośmiu pizzach! Mówimy o ośmiu kawałkach, które składają się na jedną pizzę.
i
Oczywiście w mianowniku i liczniku możemy mieć dowolne liczby całkowite. W ten sposób 1/2 to nic innego jak połowa (jedna druga – jedna z dwóch części), a 1/4 to ćwierć (jedna czwarta – jedna z czterech części).
Powiedzieliśmy, że ułamki są wszędzie i będziesz je napotykać przez całe swoje życie. Jeśli w którejś z gier komputerowych czy tych na telefonie, twoja postać wykonała trzy z siedmiu zadań do wykonania możesz śmiało powiedzieć, że wykonałeś już 3/7 swoich zadań.
Czytaj: Zamiana jednostek miar i wag. Jak zamienić kilogramy na gramy, a centymetry na metry?
Zaokrąglanie liczb: na czym polega? Jak zaokrąglić do dziesiątek, setek, tysięcy?
Pole powierzchni figury geometrycznej - jak obliczyć?
Wzory matematyczne dla ósmoklasistów i nie tylko
Dodawanie i odejmowanie ułamków zwykłych
Na ułamkach można też dokonywać działań matematycznych. Właściwie wszystkie operacje, które mogłeś wykonać na liczbach całkowitych, można wykonać na ułamkach.
Na początku powiedzmy o dodawaniu i odejmowaniu. Żeby dodawać i odejmować dwa ułamki, musimy spełnić jeden bardzo ważny warunek. Oba ułamki muszą mieć ten sam mianownik. Dlaczego? Wyobraź sobie, że podzieliłeś swoją pizzę na osiem kawałków. Każdy z kawałków to 1/8 Twojej pizzy. Twój kolega pokroił identycznej wielkości pizzę, ale aż na cztery kawałków. Jego kawałki są więc większe i każdy stanowi 1/4, czyli ćwierć całej pizzy.
i
Jeśli zbierzecie wszystkie kawałki obok siebie, to macie razem dwanaście kawałków, ale cztery z nich są większe niż osiem pozostałych i ciężko tak naprawdę ocenić, ile pizz możecie z tego ułożyć. Żeby dodawać do siebie ułamki, musicie więc upewnić się, że całość została podzielona na tyle samo części, czyli że mianownik jest taki sam.
Wtedy wystarczy, że dodasz do siebie liczniki. Jeśli tobie zostało dwa z czterech kawałków ciasta, a twojemu koledze został jeden z czterech kawałków identycznego ciasta, to razem macie trzy z czterech kawałków ciasta. Analogicznie:
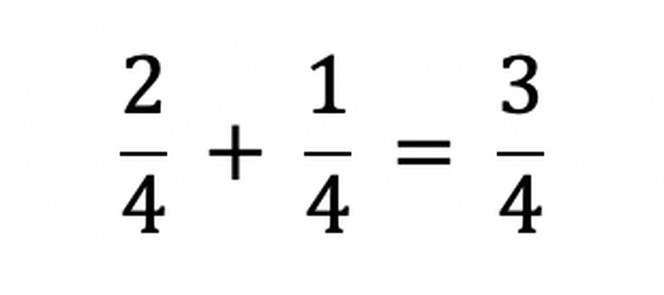
i
Sprowadzanie ułamków zwykłych do wspólnego mianownika
Niestety, jak nietrudno zauważyć, bardzo często ułamki mają różne mianowniki. Nie znaczy to jednak, że nie da się ich do siebie dodać. W takich momentach musimy sobie sami poradzić i doprowadzić ułamek do stanu, w którym będziemy mogli go dodać do innego.
Ułamki możemy np. rozszerzać. Być może zauważyłeś, że w naszym poprzednim przykładzie, że 2/4 pizzy to po prostu jej połowa (dwa z czterech kawałków). Ale przecież wcześniej ustaliliśmy, że połowa to 1/2. Czy to są jakieś różne połowy?
Nie! 1/2 i 2/4 to dokładnie ta sama liczba, tylko zapisana innym ułamkiem. Być może zauważyłeś, że do uzyskania 2/4 wystarczyło pomnożyć zarówno licznik jak i mianownik o 2. Takie właśnie mnożenie nazywamy rozszerzaniem ułamka. Licznik i mianownik możemy mnożyć i dzielić dowolnie, tak długo jak dokonujemy tych działać i na liczniku, i na mianowniku.
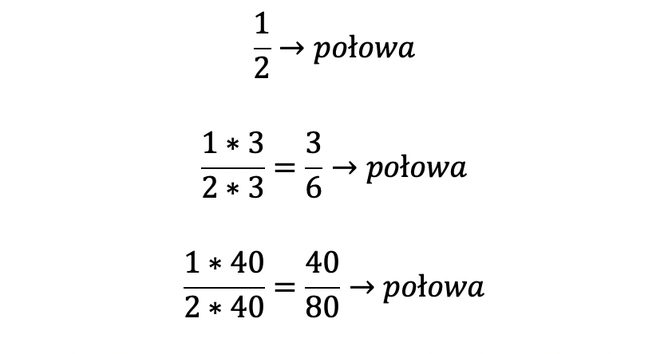
i
Dzięki temu, że mnożymy zarówno licznik, jak i mianownik, nie zmieniamy prawdziwej wartości ułamka, mimo faktu, że zmieniliśmy jego mianownik.
Dodawanie ułamków o różnych mianownikach
Spróbujmy więc dodać jakieś ułamki o różnych mianownikach.
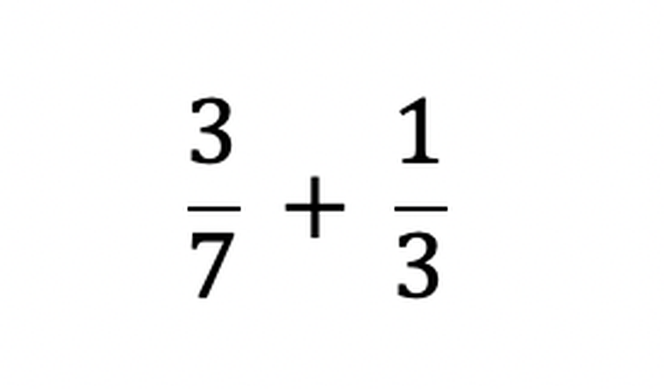
i
Naszym celem będzie sprowadzenie i jednego ułamka i drugiego do postaci, w której będą miały te same mianowniki. Trzeba tu znaleźć jakąś wspólną wielokrotność siódemki i trójki. Najłatwiej będzie rozszerzyć każdy z tych ułamków o mianownik tego drugiego.
Mianownikiem drugiego ułamka jest 3. O tyle rozszerzymy więc pierwszy ułamek i otrzymamy:
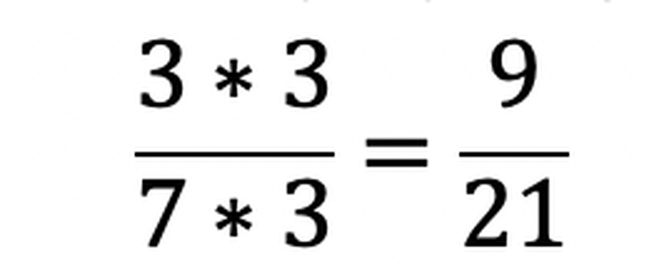
i
Choć na pierwszy rzut oka tego nie widać to 3/7 = 9/21. Mianownikiem pierwszego ułamka było 7 i znowu, o tyle rozszerzymy ułamek drugi.
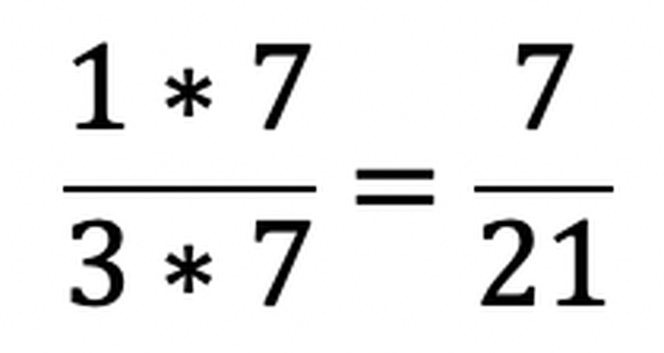
i
Nasze działanie, wygląda więc tak - bo wystarczy już dodać do siebie liczniki.
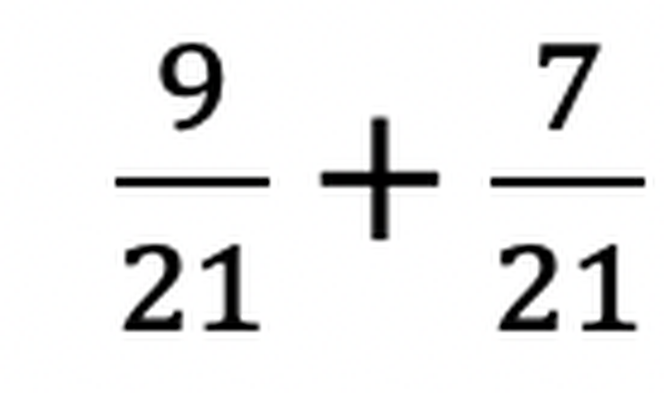
i
Ułamki niewłaściwe i liczby mieszane
Do tej pory mieliśmy do czynienia z ułamkami właściwymi, czyli takimi, które wyrażają liczbę mniejszą niż 1, albo inaczej takimi, które mają mianownik większy od licznika. Co jednak się stanie, gdy dodamy do siebie 1/3 i 3/4?
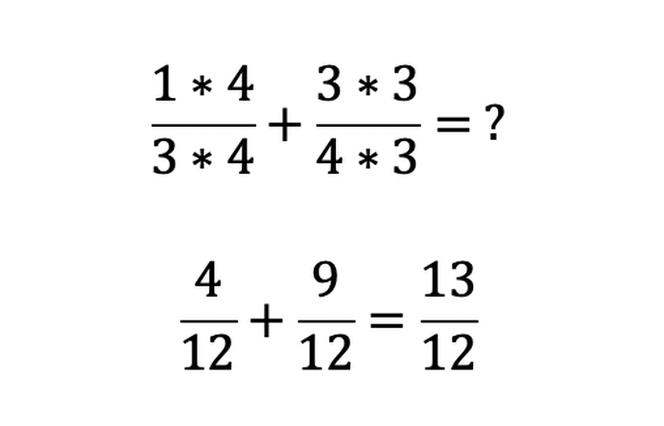
i
Taki ułamek może wyglądać jeszcze nietypowo, ale jest jak najbardziej poprawnym wynikiem tego działania. Jest to ułamek niewłaściwy. Przedstawia liczbę większą niż 1.
Jak wyglądałoby to w rzeczywistości? Wyobraź sobie dwie pizze. Jedną i drugą pokrojono na 12 kawałków. Goście zjedli łącznie 13 kawałków (4 kawałki pizzy z pieczarkami i 9 kawałków pizzy z salami). Jedna pizza to 12 kawałków, czyli 12/12, a goście zjedli jeszcze o jeden kawałek pizzy więcej. Zjedli więc jedną całą pizzę i jeden kawałek.
Możemy to zapisać za pomocą tzw. liczby mieszanej. Wyglądałoby to tak, jak poniżej, a taką liczbę czytamy jako jeden i jedna dwunasta.
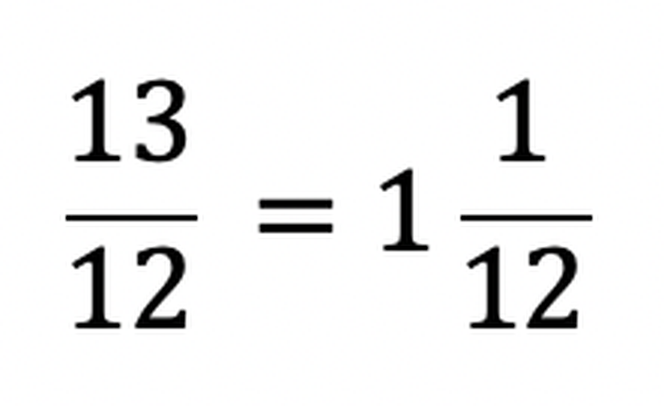
i
