Kobieta prowadzi popularne konto na Instagramie pod nazwą @matematykagryzie, które obserwuje ponad 159 tysięcy osób. Na profilu tym co rusz publikuje posty na prośby swoich obserwatorów, którzy proszą o wytłumaczenie jakieś matematycznej zawiłości. Niedawno nauczycielka została poproszona o wytłumaczenie zamiany jednostek.
Tak najszybciej nauczysz się zamiany jednostek. Matematyczka zdradza patent
Postanowiła wytłumaczyć to zagadnienie za pomocą tzw. zasady ręki. Na czym ona polega?
- Na kartce papieru należy odrysować swoją dłoń.
- Następnie każdemu z palców przypisujemy jedną jednostkę: kilometry, metry, decymetry, centymetry i milimetry.
- Między poszczególnymi palcami wpisujemy zaś wartości: 1000, 10, 10 i 10 (tak jak na poniższym zdjęciu).
- Teraz przechodzimy do zamiany jednostek, posiłkując się przygotowanym rysunkiem.
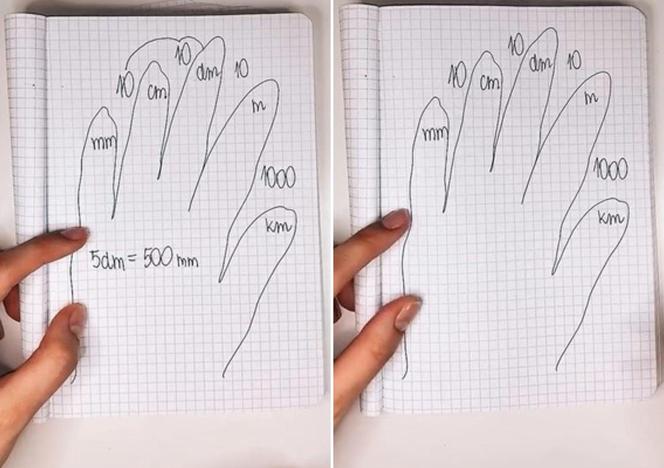
i
Jako pierwszy przykład nauczycielka podała 5 decymetrów, które zamieni na milimetry. Zasada obliczeń polega na tym, aby policzyć, ile zer znajduje się między palcem symbolizującym decymetr a milimetr. W tym przypadku są to dwa zera. Dopisujemy je do 5, otrzymując wynik 500 mm.
Jako drugi przykład instagramerka podaje zamianę w drugą stronę - z mniejszej jednostki na większą (milimetry na metry). Tu znów radzi policzyć wszystkie zera od palca symbolizującego milimetry do palca z metrami. Różnica polega tylko na tym, że zera tym razem pojawiają się nie po liczbie, tylko przed nią - dając ułamek. Tu dokładnie 3 mm dały 0,003 metra.
Internauci byli zachwyceni prostotą, z jaką matematyczka wytłumaczyła to trudne dla niejednego ucznia zagadnienie. "Sztos. Lubiłam matmę zawsze, ale przy przeliczaniu jednostek nie miałam do siebie zaufania", "Dlaczego tak mi w szkole nie tłumaczyli? Z Panią da się lubić matematykę", "Z matematyki jestem słaba, ale jak Pani tłumaczy, to chce się serio słuchać", "Uwielbiam Panią" – pisali.








