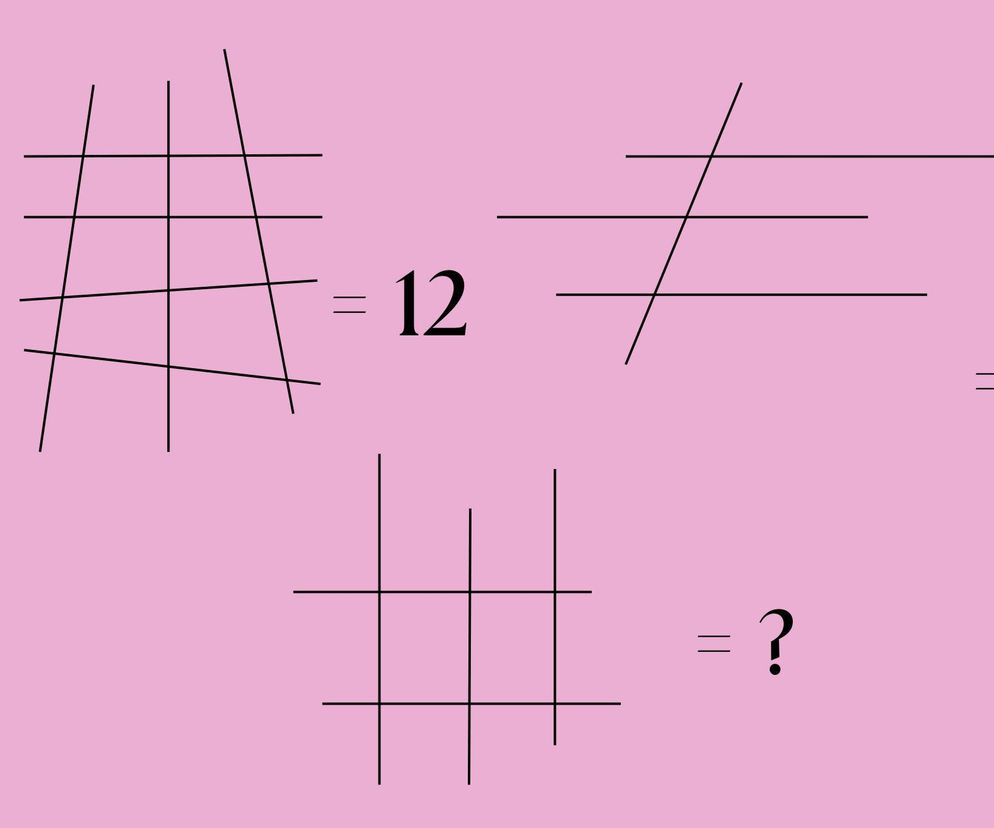Zadania logiczne są różne: to równania matematyczne, przestawianie zapałek, zagadki obrazkowe, układanie wyrazów z rozsypanych liter itp. To nie tylko sposób na nudę, ale i doskonały trening szarych komórek. Często to te najłatwiejsze łamigłówki sprawiają najwięcej trudności - rozwiązanie wydaje nam się zbyt oczywiste, aby uznać je za prawdziwe. To dlatego często dzieci radzą sobie o wiele lepiej, nie doszukują się haczyków, po prostu mówią, co wydaje im się słuszne. I dobrze na tym wychodzą.
Spis treści
Rozwiąż zagadkę logiczną
Jednym z zadań, w którym lepiej radzą sobie dzieci, jest to z liniami. Dlaczego? Z podobnymi rysunkami spotykają się w szkole, szybko orientują się w zależnościach. A ty, co widzisz? Ciągle nie zgadza ci się liczba linii z tą podaną obok?
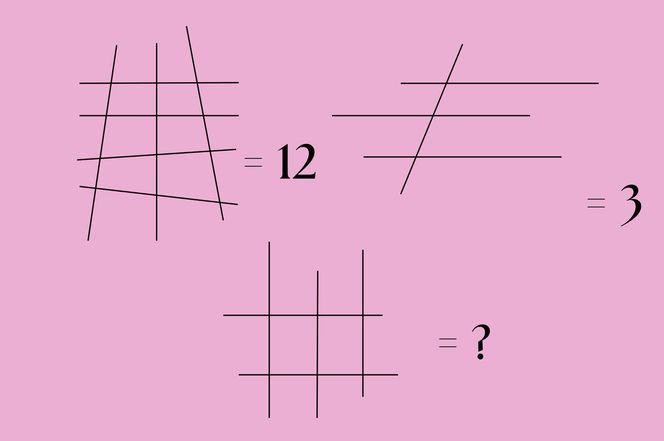
i
Nie wiesz, jak z siedmiu linii zrobiło się 12, jak cztery to nagle trzy? Popatrz jeszcze raz. Cztery poziome, trzy pionowe, jedna pionowa, trzy poziome. I w końcu - dwie poziome, trzy pionowe. Uwaga: tak, wiem, że niektóre są skośne, pozwoliłam sobie na pewną generalizację, mam nadzieję, że zostanie mi to wybaczone.
Wiesz już, o co chodzi? Popatrz na linie i zobacz, co łączy wszystkie obrazki. Na pewno zauważysz wspólne punkty (uwaga: to słowa-klucze).
Przeczytaj także: Bez liczenia na kartce poradzą sobie tylko wyjadacze. Jaki jest twój wynik?
Rozwiązanie zadania
Wiesz już, czemu dzieci od razu podają prawidłowy wynik? Bo rysowanie linii pomaga w nauce tabliczki mnożenia. Punkty przecięcia podpowiadają prawidłowy wynik.
Gdy narysujemy cztery poziome linie i przecinające je trzy pionowe, otrzymamy 12 wspólnych punktów. Zatem 4×3=12. A gdy mamy trzy poziome linie i jedną pionową, widzimy trzy punkty przecięcia. 3×1=3.
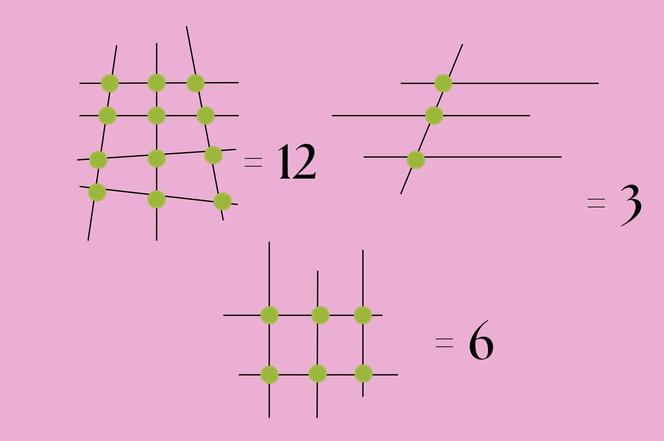
i
Teraz już wszystko powinno być jasne. Mamy wskazać, co powinno znaleźć się przy ostatnim rysunku. Mamy dwie poziome linie i trzy pionowe. To sześć punktów przecięcia. Sprawdzamy to, co oczywiste: 2×3=6. Wszystko się zgadza.
Od razu znałeś rozwiązanie, czy nie było takie oczywiste?
Przeczytaj także: To nie jest kolejna banalna zagadka matematyczna. Uda ci się, jeśli pamiętasz tę zasadę