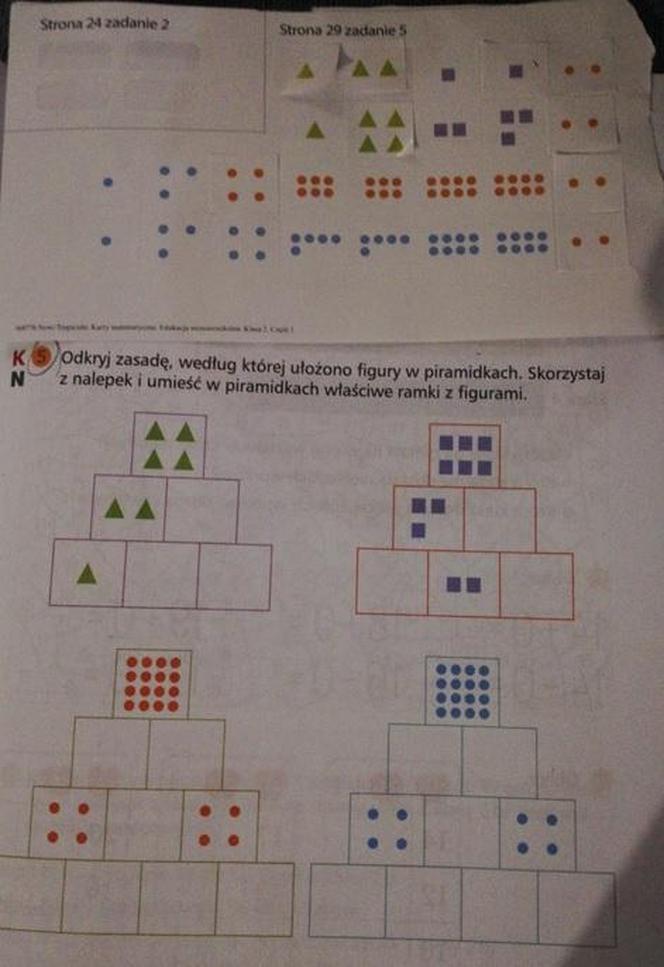
"Odkryj zasadę, według której ułożono figury w piramidkach. Skorzystaj z nalepek i umieść w piramidkach właściwe ramki z figurami" - brzmiało zadanie z matematyki dla uczniów drugiej klasy. Zadanie jest typowo logicznym wyzwaniem - na rysunku znajdują się pola, z których część jest już wypełniona, a część - wymaga dopiero wklejenia odpowiednich naklejek przez ucznia.
Zadanie było bardzo trudne dla pewnego drugoklasisty, który poprosił o pomoc ojca. Ten z kolei - po kilku próbach rozwiązania zadania, wysłał screena strony do znajomych w mediach społecznościowych, ale i ci polegli. Rozwiązanie znalazła w końcu studentka politechniki. Po jej wytłumaczeniach okazało się, że zadanie jest proste, ale wymaga odrzucenia pierwszego pomysłu, który od razu się nasuwa po spojrzeniu na rysunek.
i
Pierwsze rozwiązanie nie zawsze jest dobre
Pierwsza piramidka, która znajduje się na rysunku, zawiera 3 piętra. Na najwyższym widać 4 trójkąty, na dwóch niższych - dwa pola, jedno puste, drugie - z dwoma trójkątami. Najniższe piętro, czyli podstawa piramidki, zawiera trzy pola, z których tylko w jednym widoczny jest jeden trójkąt.
Pierwsza myśl po spojrzeniu na rysunek jest taka, że puste pole w środkowym piętrze powinno otrzymać naklejkę z 2 trójkątami - wówczas suma figur z tego poziomu będzie równa liczbie figur w górnym - to prawidłowa odpowiedź, bo na kartce znajduje się naklejka z dwoma trójkątami. Problem zaczyna się niżej - idąc tym tropem, w najniższym piętrze powinny znaleźć się 4 trójkąty, ale pól jest tylko 3.
Czytaj również: Proste zadanie matematyczne rozłożyło rodziców na łopatki. "Dzieci radzą sobie lepiej"
Matka pierwszoklasisty pokazała zadanie z matematyki. Rodzice łapią się za głowy
Prostsze niż myślisz
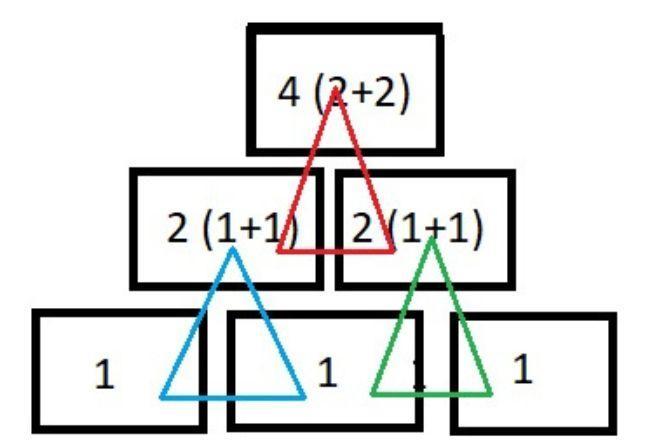
Rozwiązanie, które znalazła studentka, jest oczywiście bardzo proste, ale wymaga odrzucenia tego opisanego powyżej, które nasuwa się jako pierwsze i oczywiste. Owszem, chodzi o sumę figur, ale nie w całym piętrze, lecz w polach stanowiących podstawę pola górnego. Liczba figur w danym polu piramidki jest sumą dwóch pól w piętrze niższym.
Rozwiązanie piramidy z zielonymi trójkątami powinno być więc następujące: na szczycie - 4 trójkąty, środkowe piętro - 2 i 2 trójkąty, najniższe - po jednym trójkącie.
Podobna zasada dotyczy pozostałych piramidek. Gdy już ją znasz, wypełnienie kolejnych pustych pól naklejkami nie powinno stanowić problemu.
i








